一文读懂贝叶斯网络

作者：Devin Soni翻译：车前子 校对：孙韬淳

本文从概率论出发，为你阐述贝叶斯网络。

贝叶斯网络是一种利用贝叶斯推断进行概率计算的概率图模型。贝叶斯网络的目的是通过有向图结构中的边来表示条件依赖（conditional dependence）从而对条件依赖进行建模，并由此延伸到因果关系（causation）建模。通过这些关系并利用因子（factors），我们可对图中的随机变量进行有效推断。

概率

在讨论贝叶斯网络究竟是什么之前，我们需要先回顾一下概率论。

首先，记住随机变量A_0, A_1, …, A_n的联合概率分布。根据概率链式法则（https://en.wikipedia.org/wiki/Chain_rule_(probability)），表示为P（A_0，A_1，…，A_n）的联合概率分布等于P（A_1 | A_2，…，A_n）*P（A_2 | A_3，…，A_n）*…*P（A|n）。我们可以认为这是概率分布的 因式分解表示（factorized representation），因为它是N个局部概率的乘积（product）。

接下来回想一下，给定另一个随机变量C，两个随机变量A和B之间的 条件独立性（conditional independence）等价于满足以下性质：P（A，B | C）=P（A | C）*P（B | C）。换句话说，只要C的值是已知且固定的，A和B就是独立的。另一种表达方式是P（A | B，C）=P（A | C），我们稍后会用到。

贝叶斯网络

利用贝叶斯网络所指定的关系，我们可以利用条件独立性获得联合概率分布的紧凑的因式分解表示。

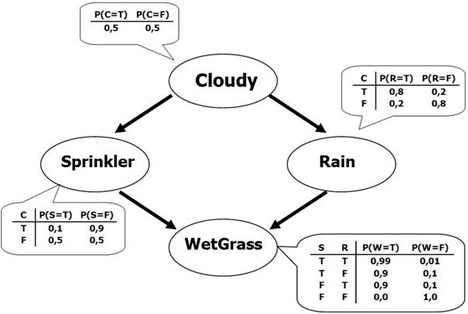
贝叶斯网络是一个有向无环图（directed acyclic graph, DAG），其中每个边对应一个条件依赖，每个节点对应一个唯一的随机变量。形式上，如果连接随机变量A和B的图中存在边（A，B），则表示P（B | A）是联合概率分布中的一个因子，因此我们必须知道对B和A所有的值而言的P（B | A）才能进行推理。在上面的示例中，由于Rain有一个边与WetGrass相连，这意味着P（WetGrass | Rain）将是一个因子，其概率值在条件概率表中WetGrass节点的旁边注明。

贝叶斯网络满足局部马尔可夫性（local Markov property）。它要求，在给定一个节点的父节点（parent）的情况下，这个节点有条件地独立于它的非子节点（non-descendant）。在上面的例子中，这意味着P（Sprinkler | Cloudy，Rain）=P（Sprinkler | Cloudy），因为给定多云的条件下，喷水器有条件地独立于其非子节点——下雨。这个性质使我们可以将上一节中使用链式规则得到的联合分布简化为更简洁的形式。经过简化后，贝叶斯网络的联合分布等于所有节点的P（节点|父节点）的乘积，如下所示：

在更大的网络中，这个属性使我们大大减少了计算量，因为一般来说，相对于网络的整体大小，大多数节点的父节点很少。

推断

贝叶斯网络的推理有两种形式。

第一种方法是简单地评估网络中每个变量（或子集）的特定赋值的联合概率。对于这一点，我们已经有了联合分布的分解形式，所以我们只是使用提供的条件概率来评估结果。如果我们只关心变量的一个子集，我们就需要将那些我们不感兴趣的变量边缘化。在许多情况下，这可能会导致下溢（译者注：意为计算机浮点数计算的结果小于可以表示的最小数），因此通常取该乘积的对数，这相当于将乘积中每个项的单个对数相加。

第二个方法更有趣的推断任务是求P（x | e），或者在给定其他变量赋值的情况下，求变量子集赋值的概率（x）（我们的证据e）。在上面的例子中，这一点的一个例子可以是找到P（Sprinkler，WetGrass | Cloudy），其中{Sprinkler，WetGrass}是我们的x，{Cloudy}是我们的e。为了计算这个，我们使用P（x | e）=P（x，e）/P（e）=αP（x，e），其中α是一个归一化常数，我们将在最后利用P（x | e）+P（¬ x | e）= 1计算。为了计算P（x，e），我们必须将x或e中没有出现的变量的联合概率分布边缘化，我们将其表示为Y。

对于给定的示例，我们可以计算这样P(Sprinkler, WetGrass | Cloudy)：

我们会以同样的方式计算P（¬ x | e），只是将x中变量的值设为false而不是true。一旦计算了P（x | e）和P(¬x | e)，我们就可以解出α，它等于 1 / (P(x | e) + P(¬x |e))。

注意，在较大的网络中，Y很可能相当大，因为大多数推断任务只会直接使用一小部分变量。在这样的情况下，如上所示的精确推断计算量非常大，因此必须使用方法来减少计算量。一种更有效的精确推断的方法是通过变量消去法（https://en.wikipedia.org/wiki/Variable_elimination），它利用了每个因素只涉及少量变量的事实。这意味着可以重新排列总和，以便只有涉及给定变量的因素才用于该变量的边缘化。或者，许多网络甚至对于这种方法来说都太大了，因此使用近似推理方法，例如MCMC（https://en.wikipedia.org/wiki/Markov_chain_Monte_Carlo）；这些方法提供的概率估计比精确推理方法所需的计算量要少得多。

原文标题：Introduction Bayesian Networks

原文链接：https://towardsdatascience.com/introduction-to-bayesian-networks-81031eeed94e

译者简介：车前子，北大医学部，流行病与卫生统计专业博二在读。从临床医学半路出家到数据挖掘，感到了数据分析的艰深和魅力。即使不做医生，也希望用数据为医疗健康做一点点贡献。

END

版权声明：本号内容部分来自互联网，转载请注明原文链接和作者，如有侵权或出处有误请和我们联系。